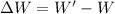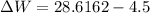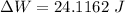Answer:
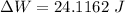
Step-by-step explanation:
Given:
- work done to stretch the spring,
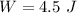
- length through which the spring is stretched beyond equilibrium,
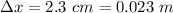
- additional stretch in the spring length,
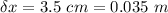
We know the work done in stretching the spring is given as:
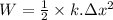
where:
k = stiffness constant
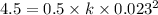
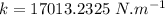
Now the work done in stretching the spring from equilibrium to (
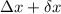 ):
):
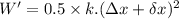
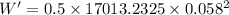
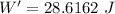
So, the amount of extra work done: