Question

team with a quality of 0.7, pressure of 1.5 bar, and flow rate of 10 kg/s enters a steam separator operating at steady state. Sat-urated vapor at 1.5 bar exits the separator at state 2 at a rate of 6.9 kg/s while saturated liquid at 1.5 bar exits the separator at state 3. Neglect-ing kinetic and potential energy effects, determine the rate of heat transfer, in kW, and its associated direction.

Answer 1

-222.649 kW

Step-by-step explanation:

The first step to solve this problem is to use the first law of thermodynamics:

`(dE)/(dt)=Q-W+\sum{m_(i)*h_(i)}-\sum{m_(e)*h_(e)}`

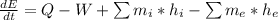
Note that Q, W, and m represent rate of heat transfer, rate of work, and mass flow rate.

This reduces to:

`0=Q-0+m_(1)h_(1)-m_(2)h_(2)-m_(3)h_(3)`

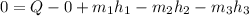
This equation can be rearranged to solve for rate of heat transfer (Q):

`Q=m_(3)h_(3)+m_(2)h_(2)-m_(1)h_(1)`

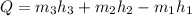
The enthalpy values for this problem can be found from tables. From Fundamentals of Engineering Thermodynamics 9th Edition, the table used was Table A-3: Properties of Saturated Water (Liquid-Vapor): Pressure Table.

The value for
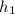`h_(1)` is found by using the equation
`h_(1)=h_(f)+x(h_(g)-h_(f))`

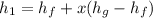
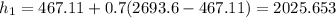`h_(1)=467.11+0.7(2693.6-467.11)=2025.653` kJ/kg

The value for
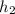`h_{2` is the value for
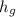`h_(g)` at 1.5 bar due to it being saturated vapor.

`h_(2)` = 2693.6 kJ/kg

The value for
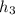`h_(3)` is the value for
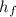`h_(f)` at 1.5 bar due to it being saturated liquid.

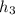`h_(3)` = 467.11 kJ/kg

Now these values can be substituted back into the equation solving for Q:

`Q=m_(3)(467.11)+m_(2)(2693.6)-m_(1)(2025.653)`

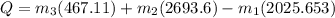
Note that
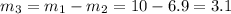`m_(3)=m_(1)-m_(2)=10-6.9=3.1` kg/s

The equation solving for Q becomes:

`Q=(3.1)(467.11)+(6.9)(2693.6)-(10)(2025.653)`

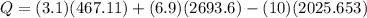
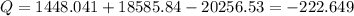`Q=1448.041+18585.84-20256.53=-222.649` kW