Answer:
Therefore the profit interval is (0,2200).
Explanation:
Given cost and revenue function are respectively,
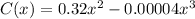
and
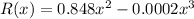
where x is the number of game sold,
 .
.
Therefore the profit function is
P(x)= R(x)-C(x)

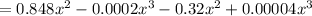

To determine the profit interval where profit function increasing, we have to find the critical point of P(x). We set the first order derivative equal to 0.
Therefore,
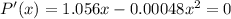
⇒x(1.056-0.00048 x) =0
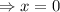 or,
or,
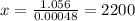
Now choose two point one is less than 2200 and other is greater than of 2200.
We choose x= 1000 and x= 2000
Now
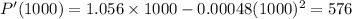 >0
>0
 <0
<0
Therefore the profit interval is (0,2200).