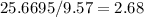Question

Consider a two-stage cascade refrigeration system operating between the pressure limits of 1.2 MPa and 200 kPa with refrigerant-134a as the working fluid. Heat rejection from the lower cycle to the upper cycle takes place in an adiabatic counterflow heat exchanger where the pressure in the upper and lower cycles are 0.4 and 0.5 MPa, respectively. In both cycles, the refrigerant is a saturated liquid at the condenser exit and a saturated vapor at the compressor inlet, and the isentropic efficiency of the compressor is 80 percent. If the mass flow rate of the refrigerant through the lower cycle is 0.15 kg/s, determine (a) the mass flow rate of the refrigerant through the upper cycle, (b) the rate of heat removal from the refrigerated space, and (c) the COP of this refrigerator.

Answer 1

Answer in detail is attached below.

Step-by-step explanation:

Answer 2

a) The mass flow rate of the refrigerant = 0.21194 kg/s

b) Heat Removal rate = 25.6695kw

c) COP = 2.682

Step-by-step explanation:

Given that

Working fluid R-134a

Exit pressure of the evaporator p1 = 200kpa

Exit pressure of the compressor for upper cycle p6 = 1.2mPa

Isotropic efficiency of compressor ηc = 0.8

Mass flow rate of the refrigerant in lower cycle m1 = 0.15kg/s

Pressure in the upper cycle heat exchanger p5 = 0.5mPa

Pressure in the lower cycle heat exchanger p3 = 0.3 mPa

State Point 1

From the saturated refrigerant -134a, pressure table

P1 = 200kPa

h1 = hg = 244.46 kJ/kg

s1 = sg = 0.93773 kJ/kg.K

State point 2

P2 = 500kPa

S2 = S1 = 0.93773kJ/kg.K

From the super heated refrigerant -134a, we do an interpolation

`h_2_s=259.30 + ((263.46-259.30)(0.93773-0.9240))/((0.9383-0.9240) \\h_2_s=263.294kJ/kg`

We can find the isotropic efficiency of the compressor

ηc=
`(h_2_s-h_1)/(h_2-h_1\\)\\0.8=(263.294-244.46)/(h_2-244.46) \\h_2=268.0025kJ/kg\\`

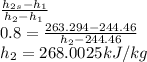
At point 3

From the saturated refrigerant -134a pressure table

when P3 = 0.5mPa

h3 = hf = 73.33 kJ/kg

for throttling,

h4 = h3 = 73.33kJ/kg

State point 5

p5 = 0.4mPa

Using the saturated refrigerant -134a pressure table

h5 = hg = 255.55kJkG

`S_5=S_g=0.9261kJ/kg.K`

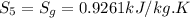
At state point 6

P6 = 1200kPa

S6 = S5 = 0.92961 kJ/kg.K

From the saturated refrigerant -134a pressure table, we can proceed to use interpolation

`h_6_s=278.27+(289.64-278.27)/(0.9614-0.9267)*(0.92691-0.9267)\\h_6_s=278.34kJ/kg`

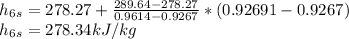
and we have ηc=
`(h_6_s-h_5)/(h_6-h_5); 0.8= (278.34-255.55)/(h_c-255.55)\\h_c=284.04kJ/kg\\h_c=h_f=117.77kJ/kg\\for throttling,\\h_8=h_7=117.77kJ/kg\\`

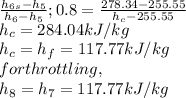
a)

The mass flow rate of the refrigerant through upper cycle can be calculated as

`M_h=(Ml(h_2-h_3))/(h_5-h_8) \\M_h=(0.15*(268.0025-73.33))/(255.55-117.77)\\M_h= 0.21194kg/s`

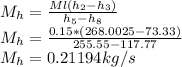
b)

The rate of heat removal from the refrigerated space

θ
`_l`=
`M_l=(h_1-h_4)\\`

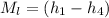
θ
`_l`=
`0.15*(244.46-73.33)\\`

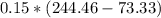
θ
`_l`=
`25.6695kw`

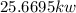
c) The COP of this refrigerator

power input W(in) =
`M_h(h_6-h_5)+m_l(h_2-h_1)\\W_i_n=0.21194*(284.04-255.55)+0.15(268.0025-244.46)\\W_i_n=9.57kw`

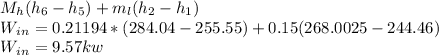
The calculated power input is 9.57kw

The COP of the refrigeration system

COP=θ
`_l`/w(in)

COP=
`25.6695/9.57=2.68`