Question

Some fireworks were projected vertically into the air from the ground at an initial velocity of 80 feet! per second. The function modeling the path of the fireworks is given as

h(t) = -16+2 + 80t where h represents the height of the fireworks t seconds after launch. How long where the

fireworks in the air before returning to the ground?

Answer 1

Therefore,

Fireworks for 5 seconds in the air before returning to the ground.

Explanation:

Given:

The function modeling the path of the fireworks is given as

`h(t)=-16t^(2)+80t`

Where,

h represents the height of the fireworks t seconds after launch.

To Find:

How long where the fireworks in the air before returning to the ground,

t = ? at h = 0

Solution:

The function modeling the path of the fireworks is given as

`h(t)=-16t^(2)+80t`

Put h(t) =0 for time t = ?

`0=-16t^(2)+80t\\\\16t(t-5)=0\\\\t = 0 \or\ t = 5`

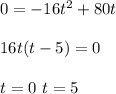
As t cannot be 0

`t = 5\ s`

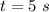
Therefore,

Fireworks for 5 seconds in the air before returning to the ground.