The approximate area of the window = 9.6 ft²
What is the approximate area of the figure (window)?
The approximate area of the window can be determined by finding the area of the semicircle and the area of the rectangle. The base of the rectangle is also the base of the semicircle.
Thus, the area of a semicircle can be calculated by using the formula:
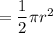
- the base(diameter) = 2 ft
- radius = d/2 = 2/2 = 1 ft
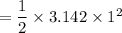
= 1.571 ft²
Area of the rectangle = length × width
Area of the rectangle = 4 ft × 2 ft
Area of the rectangle = 8 ft²
Total approximate area of the window = 1.571 ft² + 8 ft²
Total approximate area of the window = 9.571 ft²
The approximate area of the window = 9.6 ft²