Question

3. Suppose that a positive integer is written in decimal notation as n = akak-1… a2a1a0 where 0 ai 9. Prove that n is divisible by 9 if and only if the sum of its digits ak + ak–1 + … + a1 + a0 is divisible by 9.

Answer 1

Therefore n is divisible by 9 if and only if
`a_k+a_(k-1)+.........+a_1+a_0` is also divisible by 9.

Explanation:

Given number is

`n= a_ka_(k-1).....a_2a_1a_0`

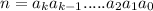
This means

`n=a_k10^k +a_(k-1)10^(k-1)+.....+a_110^1+a_0`

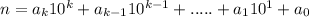
Here we need to prove

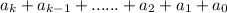`a_k+a_(k-1)+......+a_2+a_1+a_0` is divisible by 9.

We know that

10 ≡ 1 mod 9

It means if 10 divides by 9 the remainder = 1.

`n=a_k10^k +a_(k-1)10^(k-1)+.....+a_110^1+a_0`

`\Rightarrow n \equiv a_k(1)^k+a_(k-1)(1)^(k-1)+.........+a_1(1)^1+a_0` mod 9

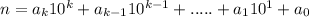
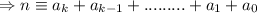`\Rightarrow n \equiv a_k+a_(k-1)+.........+a_1+a_0` mod 9

Therefore n is divisible by 9 if
`a_k+a_(k-1)+.........+a_1+a_0` is also divisible by 9.

And conversely is also true.

Therefore n is divisible by 9 if and only if
`a_k+a_(k-1)+.........+a_1+a_0` is also divisible by 9.