Answer:
y =
 x +
x +
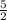
Explanation:
1. Put the given equation in Y = mx + b form
-2x-3y-5=0
-2x-5=3y
-2/3x - 5/3=y
2. Since We know that the slope of the given line is perpendicular, therefore the slope of the new line is the negative recipricol
m = 3/2 (slope of new line)
3. Find your b value by subbing in the points (-1,1)
y=mx + b
1= 3/2 (-1) + b
1= -3/2 +b
1+ 3/2 = b
5/2= b
4. write your equation
y = 3/2 x + 5/2