Answer:
40 years after 1982, there is 396.85 kilograms of radioactive element remaining. The area will not be safe for human habitation by 2022.
Explanation:
We are given the following in the question:
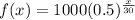
where f(x) is the amount of normal curve cannot be used as an approximation to the binomial probability. in kilograms x years after 1982.
We have to approximate f(40)
Putting x = 40, we get
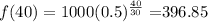
Thus, 40 years after 1982, there is 396.85 kilograms of radioactive element remaining.
With 100 kilograms of radioactive material, the area is unsafe for humans.
Thus, the area will not be safe for human habitation by 2022.