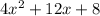The area of the rectangle is
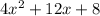
Step-by-step explanation:
Given that the height of the rectangle is 4.
The width of the rectangle is
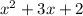
Area of the rectangle:
The area of the rectangle can be determined using the formula,
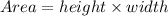
where height = 4 and width =
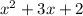
Substituting the values in the above formula, we have,
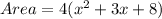
Let us expand the expression by multiplying the terms within the bracket, we get,
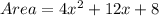
Thus, the area of the entire rectangle is