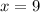Answer:
Therefore,
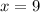
Explanation:
Given:
Let,
point L( x₁ , y₁) ≡ ( -6 , 2)
point M( x₂ , y₂ )≡ (x , 2)
l(AB) = 15 units (distance between points L and M)
To Find:
x = ?
Solution:
Distance formula between Two points is given as

Substituting the values we get

Square Rooting we get

As point M is located in the first quadrant
x coordinate and y coordinate are positive
So x = -21 DISCARDED
Hence,
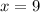
Therefore,