Question

Two ships leave a harbor together, traveling on courses that have an angle of 135°40' between them. If they each travel 402 miles how far apart are they?

Answer 1

Therefore they are 734.106 miles apart.

Explanation:

Given that ,

Two ships have a harbor together. The angle between two ships is 135°40'. Each of two ships travel 402 miles.

It forms a isosceles triangle whose two sides are 402 miles and one angle is 135°40'. Since it is isosceles triangle then other two angles of the triangle is equal.

Let ∠B= 135°40', and AB = 402 miles , BC = 402 miles

Then the distance between the ships = AC

We know

The sum of all angles = 180°

⇒∠A+∠B+∠C=180°

⇒∠A+135°40'+∠C=180°

⇒2∠A= 180°- 135°40' [ since ∠A=∠C]

⇒2∠A=44°60'

⇒∠A= 22°30'

Again we know that,

`(AB)/(sin\angle C)=(BC)/(sin \angle A)=(AC)/(sin \angle B)`

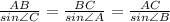
Taking last two ratio,

`(BC)/(sin \angle A)=(AC)/(sin \angle B)`

Putting the value of BC , AC ,∠A,∠B

`(402)/(sin 22^\circ30')=(AC)/(sin 135^\circ40')`

`\Rightarrow AC=(402 * sin135^\circ40')/(sin 22^\circ30')`

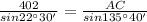
≈734.106 miles

Therefore they are 734.106 miles apart.