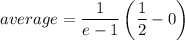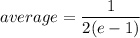Question

Find the average value of the function g(x) =
`(lnx)/(x)` over the interval [1, e].

Answer 1

`\displaystyle average=(1)/(2(e-1))`

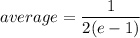
Explanation:

Average Value of a Function

Given a function g(x), we can compute the average value of g in a given interval (a,b) with the equation:

`\displaystyle average=(1)/(b-a)\int_(a)^(b) g(x)dx`

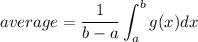
We use the given data

`\displaystyle average=(1)/(e-1)\int_(1)^(e) (lnx)/(x)dx`

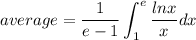
We now compute the indefinite integral with a u-substitution

`\displaystyle I=\int (lnx)/(x)dx`

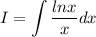
We'll use the substitution u=lnx, du=dx/x. Then

`\displaystyle I=\int u.du`

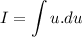
Integrating

`\displaystyle I=(u^2)/(2)`

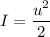
Since u=lnx

`\displaystyle I=(ln^2x)/(2)`

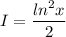
The average value is

`\displaystyle average=(1)/(e-1)\left|(ln^2x)/(2) \right|_1^e`

`\displaystyle average=(1)/(e-1)\left((ln^2e)/(2)-(ln^21)/(2) \right )`

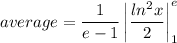
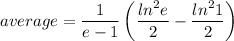
Since lne=1, and ln1=0

`\displaystyle average=(1)/(e-1)\left((1)/(2)-0 \right )`

`\displaystyle average=(1)/(2(e-1))`