Question

The free lower end of the rope is struck sharply at time t=0. What is the time t it takes the resulting wave on the rope to travel to the ceiling, be reflected, and return to the lower end of the rope? Express your answer in terms of L and constants such as g (the magnitude of the acceleration due to gravity), π, etc.

Answer 1

`t=2\sqrt{(L)/(g)}`

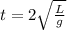
Step-by-step explanation:

The equation of the velocity of wave is given by:

`v=\sqrt{(T)/(\mu)}`

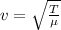
Here:

• μ is the mass per length unit (μ=m/L).

• T is the tension in each point of the rope with a specific velocity. (T=mg=μyg)

So the velocity will be:

`v=\sqrt{(\mu yg)/(\mu)}=√(yg)`

We know that the velocity is the variation of the position with respect to time so:

`v=(dy)/(dt)=√(yg)`

`(dy)/(√(yg))=dt`

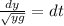
Let's take the integral in both sides:

`\int^(t)_(0)dt=\int^(L)_(0)(dy)/(√(yg))`

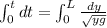
Solving these two integrals we have:

`t=2\sqrt{(y)/(g)}|^(L)_(0)=2\sqrt{(L)/(g)}`

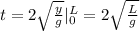
Therefore the time will be
`2\sqrt{(L)/(g)}`

I hope it helps you!