Question

After heating up in a teapot, a cup of hot water is poured at a temperature of

20
8
∘
208
∘
F. The cup sits to cool in a room at a temperature of
6
8
∘
68
∘
F. Newton's Law of Cooling explains that the temperature of the cup of water will decrease proportionally to the difference between the temperature of the water and the temperature of the room, as given by the formula below:
T
=
T
a
+
(
T
0
−
T
a
)
e
−
k
t
T=T
a
​
+(T
0
​
−T
a
​
)e
−kt

T
a
=
T
a
​
= the temperature surrounding the object
T
0
=
T
0
​
= the initial temperature of the object
t
=
t= the time in minutes
T
=
T= the temperature of the object after
t
t minutes
k
=
k= decay constant

The cup of water reaches the temperature of
18
5
∘
185
∘
F after 3 minutes. Using this information, find the value of
k
k, to the nearest thousandth. Use the resulting equation to determine the Fahrenheit temperature of the cup of water, to the nearest degree, after 4 minutes.

Enter only the final temperature into the input box.

Answer 1

• k ≈ 0.060
• T(4) ≈ 178 °F

Explanation:

The desired formula parameters for Newton's Law of Cooling can be found from the given data. Then the completed formula can be used to find the temperature at the specified time.

__

Given:

`T(t)=T_a+(T_0-T_a)e^(-kt)\\\\T_a=68,\ T_0=208,\ (t,T)=(3,185)`

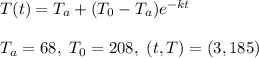
Find:

k

T(4)

Solution:

Filling in the given numbers, we have ...

185 = 68 +(208 -68)e^(-k·3)

117/140 = e^(-3k) . . . . . subtract 68, divide by 140

ln(117/140) = -3k . . . . . . take natural logarithms

k = ln(117/140)/-3 ≈ 0.060

__

The temperature after 4 minutes is about ...

T(4) = 68 +140e^(-0.060·4) ≈ 68 +140·0.787186

T(4) ≈ 178.205

After 4 minutes, the final temperature is about 178 °F.