Question

A contractor is building the base of a circular fountain. On the blueprint, the base of the fountain as a diameter of 18 cm. The blueprint has a scale of 3 cm to 4 ft. What will be the actual are of the base of the fountain in square feet after it is built? Round your answer to the nearest tenth of a square foot.

Answer 1

It's 452.4 if you use pi

Explanation:

This is a ny state test, you're not allowed to use 3.14. So, according to the state test, it would be 452.4 following all the steps of the answer above or below which is verified but you just use pi insted of 3.14.

Answer 2

The actual area of the base of the fountain will be 452.2 square feet.

Explanation:

Given:

A contractor is building the base of a circular fountain.

Diameter of the base of the fountain on the blueprint is 18 cm.

The blueprint has a scale of 3 cm to 4 ft.

Now, to find after the base of the fountain is built its actual area in square feet.

Let the actual diameter of the base of the fountain be
`x.`

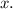
On the blueprint diameter the base of the fountain = 18 cm.

As the blueprint has scale of 3 cm to 4 ft.

According to which, 3 cm is equivalent to 4 ft.

Thus, 18 cm is equivalent to
`x.`

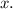
Now, to get the actual diameter of the base of the fountain by using cross multiplication method:

`(3)/(4) =(18)/(x)`

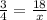
By cross multiplying we get:

`3x=72`

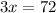
Dividing both sides by 3 we get:

`x=24.`

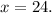
Hence, the actual diameter of the base of the fountain is 24 ft.

Now, getting the actual area of the base of the fountain by putting formula:

Diameter of the base of the fountain = 24 ft.

So, radius (r) =
`(diameter)/(2)` =
`(24)/(2)=12\ ft.`

`Area=\pi r^2`

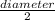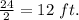
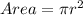
Using, π = 3.14.

`Area=3.14* 12^2`

`Area=3.14* 144`

`Area=452.16\ square\ feet.`

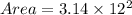
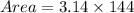
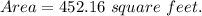
Rounding the area to the nearest tenth is 452.2 square feet.

Therefore, the actual area of the base of the fountain will be 452.2 square feet.