Answer:
The actual area of the base of the fountain will be 452.2 square feet.
Explanation:
Given:
A contractor is building the base of a circular fountain.
Diameter of the base of the fountain on the blueprint is 18 cm.
The blueprint has a scale of 3 cm to 4 ft.
Now, to find after the base of the fountain is built its actual area in square feet.
Let the actual diameter of the base of the fountain be
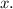
On the blueprint diameter the base of the fountain = 18 cm.
As the blueprint has scale of 3 cm to 4 ft.
According to which, 3 cm is equivalent to 4 ft.
Thus, 18 cm is equivalent to
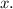
Now, to get the actual diameter of the base of the fountain by using cross multiplication method:
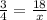
By cross multiplying we get:
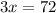
Dividing both sides by 3 we get:
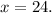
Hence, the actual diameter of the base of the fountain is 24 ft.
Now, getting the actual area of the base of the fountain by putting formula:
Diameter of the base of the fountain = 24 ft.
So, radius (r) =
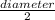 =
=
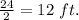
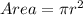
Using, π = 3.14.
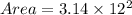
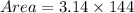
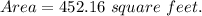
Rounding the area to the nearest tenth is 452.2 square feet.
Therefore, the actual area of the base of the fountain will be 452.2 square feet.