Question

State if the point (-3, -2) is a solution to the system of equations below.

x^2 + y^2 + x - 10y - 3=0
x+y= -4

A) Since (-3,-2) does satisfy both equations, it is a solution to the system.

B) Since (-3,-2) does not satisfy both equations, it is not a solution to the
system.

C) Since (-3,-2) does satisfy both equations, it is not a solution to the system.

D) Since (-3,-2) does not satisfy both equations, it is a solution to the system.​

Answer 1

B) Since (-3,-2) does not satisfy both equations, it is not a solution to the

system.

Explanation:

The given system of equations is:

`{x}^(2) + {y}^(2) + x - 10y - 3 = 0`

`x + y = - 4`

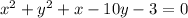
If (-3,-2) is a solution, then it must satisfy both equations:

Let us substitute into the first equation to get:

`{( - 3)}^(2) + {( - 2)}^(2) + ( - 3) - 10( - 2) - 3 = 0`

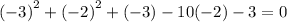
Evaluate the exponents;

`9 + 4 - 3 + 20- 3 = 0`

`27 = 0`

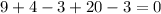
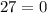
This is not true

Also when we substitute into the scond equation, we get;

`- 3 + - 2 = - 4 \\ - 5 = - 4`

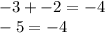
This is also false.

Therefore the point is not a solution.