Question

When 10 is subtracted from the square of a number, the result is 3 times the number. Find the negative solution.

Answer 1

Explanation:

Let the required number be x.

Therefore, according to the given condition:

`{x}^(2) - 10 = 3x \\ \therefore \: {x}^(2) - 3x - 10 = 0 \\ \therefore \: {x}^(2) - 5x + 2x - 10 = 0 \\ \therefore \: x(x - 5) + 2(x - 5) = 0 \\ \therefore \: (x - 5)(x + 2) = 0 \\ \therefore \: x - 5 = 0 \: \: or \: \: x + 2 = 0 \\ \therefore \: x = 5 \: \: or \: \: x = - 2 \\`

Therefore, x = - 2 is the negative solution.

Answer 2

Good morning ☕️

Answer:

the negative solution is -2

Explanation:

First ,we need to model the situation by expressing it as an equation

so, let x represent the uncknown negative number :

We get

x² - 10 = 3x

then

x² - 3x - 10 = 0

now using the quadratic formula:

Let Δ be the discriminant

Δ = b² - 4ac = (-3)² - 4(1)(-10) = 9 + 40 = 49 → √∆ = 7

Therefore

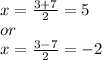
`x = (3+7)/(2)=5 \\or\\x= (3-7)/(2)=-2`

_______________________________________

:)