Answer:
The wire would need 2546 turns to produce the same magnetic field as solenoid
Step-by-step explanation:
Given;
magnetic field strength, B = 0.1 T
diameter of solenoid, d = 2 cm, radius, r = 1 cm
length of solenoid, L = 8 cm
current in the wire, I = 2.5 A
Magnetic field inside solenoid = μ₀nI
Magnetic field for circular loop = (μ₀I / 2πr)
For equal magnetic field in solenoid and circular loop;
0.1 T = μ₀nI
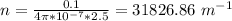
Number of loops, N = nL
N = 31826.86 m⁻¹ * 0.08 m = 2546 turns
Therefore, the wire would need 2546 turns to produce the same magnetic field as solenoid.