Question

You put half of your money in a stock portfolio that has an expected return of 14% and a standard deviation of 24%. You put the rest of your money in a risky bond portfolio that has an expected return of 6% and a standard deviation of 12%. The stock and bond portfolios have a correlation of .55. The standard deviation of the resulting portfolio will be ________________.

Answer 1

16.09 %

Step-by-step explanation:

stock portfolio expected return = 14%

stock portfolio standard deviation = 24% ( Sₐ )

Risky bond portfolio expected return = 6%

Risky bond portfolio standard deviation = 12% ( S₂ )

correlation between investments = 0.55 ( r )

To calculate the standard deviation of the resulting portfolio we will have the find the resulting Variance of the new portfolio

Resulting variance = ( Wₐ² * Sₐ²) +( Wₐ² * S₂²) +( 2 * Wₐ * Sₐ * Wₐ * S₂* r)

Wₐ = the weight of the of portfolio since equal amounts are invested hence it will be 50% for each = 0.5

Resulting variance = ( 0.5² * 0.24²) + ( 0.5² * 0.12²) + 2 ( 0.5 * 0.24 *0.5 * 0.12 * 0.55 )

= 0.2592

hence the resulting standard deviation =
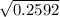`√(0.2592)` = 0.16099 = 16.09%

Answer 2

The standard deviation = 16.1%

Step-by-step explanation:

The standard deviation will be between more than 12% but less than 18%

σ2p = .02592 = (.52)(.242) + (.52)(.122) + 2(.5)(.5)(.24)(.12).55 = .02592; σ = 16.1%