Answer:
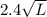 where L is the length of the ramp
where L is the length of the ramp
Step-by-step explanation:
Let L (m) be the length of the ramp, and g = 9.81 m/s2 be the gravitational acceleration acting downward. This g vector can be split into 2 components: parallel and perpendicular to the ramp.
The parallel component would have a magnitude of
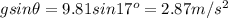
We can use the following equation of motion to find out the final velocity of the book after sliding L m:
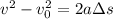
where v m/s is the final velocity,
 = 0m/s is the initial velocity when it starts from rest, a = 2.87 m/s2 is the acceleration, and
= 0m/s is the initial velocity when it starts from rest, a = 2.87 m/s2 is the acceleration, and
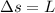 is the distance traveled:
is the distance traveled:

