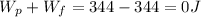Question

A factory worker pushes a crate of mass 31.0 kg a distance of 4.35 m along a level floor at constant velocity by pushing horizontally on it. The coefficient of kinetic friction between the crate and floor is 0.26.

a. What magnitude of force must the worker apply?
b. How much work is done on the crate by this force?
c. How much work is done on the crate by friction?
d. How much work is done on the crate by the normal force? By gravity?
e. What is the total work done on the crate?

Answer 1

(A) 79N

(B) W = 344J

(C) Wf= -344J

(D) W = 0J

(E) W = 0J

Step-by-step explanation:

Please see attachment below.

Answer 2

a. 79.1 N

b. 344 J

c. 344 J

d. 0 J

e. 0 J

Step-by-step explanation:

a. Since the crate has a constant velocity, its net force must be 0 according to Newton's 1st law. The push force
`F_p` by the worker must be equal to the friction force
`F_f` on the crate, which is the product of friction coefficient μ and normal force N:

Let g = 9.81 m/s2

`F_p = F_f = \mu N = \mu mg = 0.26 * 31 * 9.81 = 79.1 N`

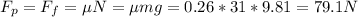
b. The work is done on the crate by this force is the product of its force
`F_p` and the distance traveled s = 4.35

`W_p = F_ps = 79.1*4.35 = 344 J`

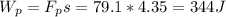
c. The work is done on the crate by friction force is also the product of friction force and the distance traveled s = 4.35

`W_f = F_fs = -79.1*4.35 = -344 J`

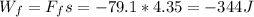
This work is negative because the friction vector is in the opposite direction with the distance vector

d. As both the normal force and gravity are perpendicular to the distance vector, the work done by those forces is 0. In other words, these forces do not make any work.

e. The total work done on the crate would be sum of the work done by the pushing force and the work done by friction

`W_p + W_f = 344 - 344 = 0 J`