Question

We would like to estimate how quickly the non-uniformities in gas composition in the alveoli are damped out. Consider an alveolus to be spherical with a diameter of 0.1mm. Let the sphere have an initial uniform concentration of oxygen, ci, and at a certain instant, the walls of the alveolus are raised to an oxygen concentration of c¥ and maintained at this value. If the oxygen diffusivity in the alveolus is approximated as that of water, 2.4x10-9 m2 /s, how long does it take for the concentration change (c-ci) at the center to be 90% of the final concentration change?

Answer 1

Answer: It will take 11.775 seconds.

Explanation: As a sphere with a diameter of 0.1 mm, the area of an alveolus is

A = 4.π.r²

r for an alveolus would be: r = 0.00005m or r = 5.
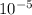`10^(-5)`m

Finding the area:

A = 4.3.14.(5.
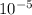`10^(-5)`)²

A = 3.14.
`10^(-8)`m²

The concentration change is to be 90% of the final, so

c = 0.9.3.14.
`10^(-8)`

c = 28.26.
`10^(-9)`

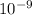
The oxygen diffusivity is 2.4.
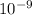`10^(-9)`m²/s, that means in 1 second 2.4.
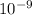`10^(-9)` of oxygen spread in one alveolus area. So:

1 second = 2.4.
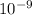`10^(-9)`m²

t seconds = 28.26.
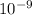`10^(-9)`m²

t =
`(28.26.10^(-9) )/(2.4.10^(-9) )`

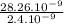
t = 11.775s

For a concentration change at the center to be 90%, it will take 11.775s.