Question

Assume the random variable X has a binomial distribution with the given probability of obtaining a success. Find the following probability, given the number of trials and the probability of obtaining a success. Round your answer to four decimal places. P(X=17), n=18, p=0.9

Answer 1

P(X=17) = 0.3002 .

Explanation:

We are given that the random variable X has a binomial distribution with the given probability of obtaining a success.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

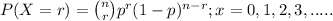
where, n = number of trials (samples) taken = 18

r = number of success = 17

p = probability of success which in our question is given as 0.9 .

So, X ~
`Binom(n=18,p=0.9)`

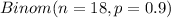
We have to find the probability of P(X = 17);

P(X = 17) =
`\binom{18}{17}0.9^(17) (1-0.9)^(18-17)`

=
`18 * 0.9^(17) * 0.1^(1)` {
`\because \binom{n}{r} = (n!)/(r! * (n-r)!)` }

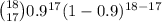
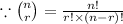= 0.3002

Therefore, P(X=17) = 0.3002 .

Answer 2

P(X = 17) = 0.3002

Explanation:

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

In this problem we have that:

`n = 18, p = 0.9`

We want P(X = 17). So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 17) = C_(18,17).(0.9)^(17).(0.1)^(1) = 0.3002`

P(X = 17) = 0.3002