Answer:
90% confidence interval for p is [0.4542 , 0.5105] .
Explanation:
We are given that a local board of education conducted a survey of residents in the community concerning a property tax levy on the coming local ballot. Of the 850 residents surveyed, 410 supported the property tax levy.
Let p = proportion of residents in the community that support the property tax levy
 = proportion of residents in the community that support the property tax levy in a survey of 850 residents =
= proportion of residents in the community that support the property tax levy in a survey of 850 residents =
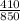 =
=
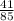
The pivotal quantity that will be used here population proportion p is;
P.Q. =
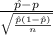 ~ N(0,1)
~ N(0,1)
So, 90% confidence interval for p is given by;
P(-1.6449 < N(0,1) < 1.6449) = 0.90 {At 10% significance level the z table give
critical value of 1.6449)
P(-1.6449 <
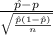 < 1.6449) = 0.90
< 1.6449) = 0.90
P(
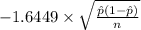 <
<
 <
<
 ) = 0.90
) = 0.90
P(
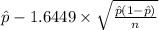 < p <
< p <
 ) = 0.90
) = 0.90
90% confidence interval for p = [
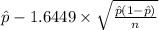 ,
,
 ]
]
= [
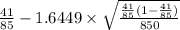 ,
,
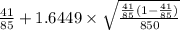 ]
]
= [ 0.4542 , 0.5105 ]
Therefore, 90% confidence interval for p is [0.4542 , 0.5105] .