Question

A polarized light is incident on several polarizing disks whose planes are parallel and centered on common axis. Suppose that the transmission axis of the first polarizer is rotated 20° relative to the axis of polarization of the incident light, and that the transmission axis of each additional analyzer is rotated 20° relative to the transmission axis of the previous one. What is the maximum number of polarizer needed (whole number), so the transmitted light through all polarizing sheets has an intensity that is equal at least 12% that striking the first polarizer?

Answer 1

The number of polarizer needed so transmitted light has at least 12% intensity = 17

Step-by-step explanation:

Given :

Angle between incident light and optic axis of polarizer = 20°

Given that, the transmission axis of each additional analyzer is rotated 20° relative to the transmission axis of the previous one

According to the malus law,

The intensity of the transmitted light passes through the polarizer is proportional to the square of the cosine of angle between the transmission axis to the optic axis.

⇒
`I = I_(o) cos^(2) \alpha`

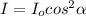
Where,
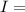`I =` transmitted intensity through polarizer,
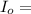`I_(o) =` incident intensity of the light.

Given in question, all the time
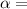`\alpha =` 20°

By calculation ∴
`cos^(2) 20 = 0.883`

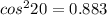
After 1st polarizer,

∴
`I_(1) = 0.883I_(o)`

Now we need to multiply all the time 0.883 until we get 0.12 (relative 20° angle given in question)

After 17th polarizer we get 0.1205 ≅ 0.12

`I_(17) = 0.883^(17) = 0.1205 * 100 = 12`%
`I_(o)`

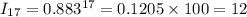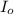
Means we get 12% intensity after 17th polarizing disk.