Question

Military radar and missile detection systems are designed to warn a country of an enemy attack. A reliability question is whether a detection system will be able to identify an attack and issue a warning. Assume that a particular detection system has a 0.80 probability of detecting a missile attack. Use the binomial probability distribution to answer the following questions. (a) What is the probability that a single detection system will detect an attack

Answer 1

0.8 is the probability that a single detection system will detect a missile attack.

Explanation:

We are given the following information:

We treat detection a missile attack as a success.

P(detecting a missile attack) = 80% = 0.8

Then the number of missile attack follows a binomial distribution, where

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

where n is the total number of observations, x is the number of success, p is the probability of success.

Now, we are given n = 1

We have to evaluate:

`P(x = 1)\\= \binom{1}{1}(0.8)^1(1-0.8)^0\\= 0.8`

0.8 is the probability that a single detection system will detect a missile attack.

Answer 2

(a) Probability that a single detection system will detect an attack is 0.80

Explanation:

We are given that a reliability question is whether a detection system will be able to identify an attack and issue a warning. Assuming that a particular detection system has a 0.80 probability of detecting a missile attack.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

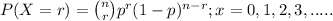
where, n = number of trials(samples) taken = 1 detection system

r = number of success

p = probability of success which in our question is probability of

detecting a missile attack, i.e., 80%

LET X = a particular detection system

Also, it is given that a single detection system is taken,

So, it means X ~
`Binom(n=1,p= 0.80)`

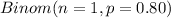
Now, Probability that a single detection system will detect an attack is given by = P(X = 1)

P(X = 1) =
`\binom{1}{1}0.8^(1) (1-0.8)^(1-1)`

=
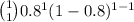
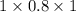`1 * 0.8 * 1` = 0.80 .