Question

A 62.0 kg skier is moving at 6.90 m/s on a frictionless, horizontal, snow-covered plateau when she encounters a rough patch 4.50 m long. The coefficient of kinetic friction between this patch and her skis is 0.300. After crossing the rough patch and returning to friction-free snow, she skis down an icy, frictionless hill 2.50 m high.

How fast is the skier moving when she gets to the bottom ofthe hill?

Answer 1

Step-by-step explanation:

mass, m = 62 kg

initial velocity, u = 6.9 m/s

length, l = 4.5 m

height, h = 2.5 m

coefficient of friction, μ = 0.3

Final kinetic energy + final potential energy = initial kinetic energy + initial potential energy + wok done by friction

Let the final velocity is v.

0.5 mv² + 0 = 0.5 mu² + μmgl + mgh

0.5 v² = 0.5 x 6.9 x 6.9 + 0.3 x 9.8 x 4.5 + 9.8 x 2.5

0.5 v² = 23.805 + 13.23 + 24.5

v² = 123.07

v = 11.1 m/s

Answer 2

Step-by-step explanation:

The given data is as follows.

Mass, m = 62 kg, Initial speed,
`v_(1)` = 6.90 m/s

Length of rough patch, L = 4.50 m, coefficient of friction,
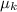`\mu_(k)` = 0.3

Height of inclined plane, h = 2.50 m

According to energy conservation equation,

(Final kinetic energy) + (Final potential energy) = Initial kinetic energy + Initial potential energy - work done by the friction

`K.E_(2) + U_(2) = K.E_(1) + U_(1) - W_(f)`

`(1)/(2)mv^(2)_(2) + U_(2) = (1)/(2)mv^(2)_(1) + mgh - \mu_(k)mgL`

Since, final potential energy is equal to zero. Therefore, the equation will be as follows.

`(1)/(2)mv^(2)_(2) = (1)/(2)mv^(2)_(1) + mgh - \mu_(k)mgL`

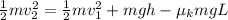
Cancelling the common terms in the above equation, we get

`(1)/(2)v^(2)_(2) = (1)/(2)v^(2)_(1) + gh - \mu_(k)gL`

=
`(1)/(2)(6.90)^(2)_(1) + 9.8 m/s^(2) * 2.50 m - (0.3 * 9.8 * 4.50 m)`

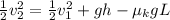
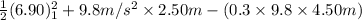
= 36.055 - 13.23

= 22.825

`v_(2) = √(2 * 22.825)`

= 6.75 m/s

Thus, we can conclude that the skier is moving at a speed of 6.75 m/s when she gets to the bottom of the hill.