Answer:
(a). The trip take a time is 3.61 year.
(b). The trip take a time is 3.96 year.
(c). The trip take a time is 8.73 year.
Step-by-step explanation:
Given that,
Length = 1.60 ly
Speed of spaceships= 0.800c
Speed of messenger = 0.910 c
(a). We need to calculate the velocity of armada
Using formula of velocity

Put the value into the formula
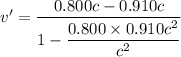

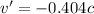
We need to calculate the length
Using formula of length

Put the value into the formula
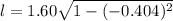
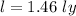
We need to calculate the length of the trip
Using formula of time
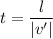
Put the value into the formula
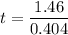
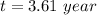
(b). If the armada's rest frame
We need to calculate the length
Using formula of length

Put the value into the formula

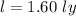
Using formula of time
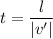
Put the value into the formula
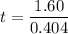
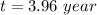
(c). If an observer in frame S
We need to calculate the length
Using formula of length

Put the value into the formula
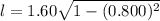
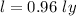
We need to calculate the time

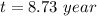
Hence, (a). The trip take a time is 3.61 year.
(b). The trip take a time is 3.96 year.
(c). The trip take a time is 8.73 year.