Question

When five basketball players are about to have a​ free-throw competition, they often draw names out of a hat to randomly select the order in which they shoot. What is the probability that they shoot free throws in alphabetical​ order? Assume each player has a different name. ​P(shoot free throws in alphabetical ​order)equals nothing ​(Type an integer or a simplified​ fraction.)

Answer 1

1/120

Explanation:

Since the players have different names, there is only one possible arrangement in which they are in alphabetical order. The total number of ways to order 5 basketball players (n) is:

`n = 5!=5*4*3*2*1\\n=120`

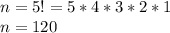
Therefore, there is a 1/120 probability that they shoot free throws in alphabetical​ order.