Question

The demand x is the number of items that can be sold at a price of​ $p. For x equals p cubed minus 7 p squared plus 600 commax=p3−7p2+600, find the rate of change of p with respect to x by differentiating implicitly.

Answer 1

1 ÷ [p(3p - 14)] = (dp/dx)

Step-by-step explanation:

Given that,

Demand equation is as follows:

`x=p^(3)-7p^(2)+600`

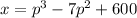
where,

x is the number of items sold

$p is the selling price of the items

Now, differentiating the above equation with respect to 'x',

`1 = 3p^(2)(dp)/(dx) - 14p(dp)/(dx) + 0`

`1=(dp)/(dx)p(3p-14)`

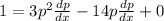
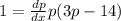
1 ÷ [p(3p - 14)] = (dp/dx)

Therefore, the rate of change of p with respect to x by differentiating implicitly is 1 ÷ [p(3p - 14)] = (dp/dx)