Question

A railroad car having a mass of 17.5 Mg is coasting at 1.5 m/s on a horizontal track. At the same time another car having a mass of 12 Mg is coasting at 0.75 m/s in the opposite direction. The cars meet and couple together.

Determine the speed of both cars just after the coupling.

Answer 1

The speed of both cars just after the coupling is 0.584 m/s.

Step-by-step explanation:

Given that,

Mass of car = 17.5 Mg

Speed of car= 1.5 m/s

Mass of another car = 12 Mg

Speed of another car = 0.75 m/s

We need to calculate the speed of both cars just after the coupling

Using conservation of momentum

`m_(1)u_(1)+m_(2)u_(2)=(m_(1)+m_(2))v`

`v=(m_(1)u_(1)+m_(2)u_(2))/((m_(1)+m_(2)))`

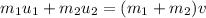
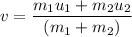
Where, m₁ = mass of one car

m₂ = mass of another car

v₁ = velocity of one car

v₂ = velocity of another car

Put the value into the formula

`v=(17.5*10^(3)*1.5-12*10^(3)*0.75)/(17.5*10^(3)+12*10^(3))`

`v=0.584\ m/s`

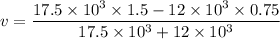
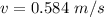
Hence, The speed of both cars just after the coupling is 0.584 m/s.

Answer 2

Then final velocity of the coupled system of cars will be 0.58 m/s

Explanation: Let us consider the car-1 is moving towards right (say + ve direction) and car-2 is moving towards left (say in - ve direction), accordingly velocity are considered +ve and -ve.

`m_(1) = 17.5 \ Mg = 17.5 * 10^(6) \ g = 17.5 * 10^(3) \ Kg = 17500 \ Kg`

`v_(1) = + \ 1.5 \ m/s`

`m_(2) = 12 \ Mg = 12 * 10^(6) \ g = 12 * 10^(3) \ Kg = 12000 \ Kg`

`v_(2) = - \ 0.75 \ m/s`

Applying the conservation of momentum, and let the final velocity of combined system is V m/s

`m_(1) * v_(1) + m_(2) * v_(2) = (m_(1) + m_(2)) * V`

`17500 * 1.5 \ + 12000 * (-0.75) = 29500 * V`

26250 - 9000 = 29500
`*` V

V =
`(17250)/(29500)` = 0.58 m/s

Then final velocity of the coupled system of cars will be 0.58 m/s