Answer:
The speed of both cars just after the coupling is 0.584 m/s.
Step-by-step explanation:
Given that,
Mass of car = 17.5 Mg
Speed of car= 1.5 m/s
Mass of another car = 12 Mg
Speed of another car = 0.75 m/s
We need to calculate the speed of both cars just after the coupling
Using conservation of momentum
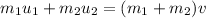

Where, m₁ = mass of one car
m₂ = mass of another car
v₁ = velocity of one car
v₂ = velocity of another car
Put the value into the formula

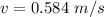
Hence, The speed of both cars just after the coupling is 0.584 m/s.