Question

A certain parallel-plate capacitor is filled with a dielectric for which k ???? 5.5. The area of each plate is 0.034 m2, and the plates are separated by 2.0 mm. The capacitor will fail (short out and burn up) if the electric field between the plates exceeds 200 kN/C. What is the maximum energy that can be stored in the capacitor?

Answer 1

The maximum energy that can be stored in the capacitor is 6.62 x 10⁻⁵ J

Step-by-step explanation:

Given;

dielectric constant k = 5.5

the area of each plate, A = 0.034 m²

separating distance, d = 2.0 mm = 2 x 10⁻³ m

magnitude of the electric field = 200 kN/C

Capacitance of the capacitor is calculated as follows;

`C = (k \epsilon A)/(d) = (5.5*8.85*10^(-12)*0.034)/(2*10^(-3)) = 8.275 *10^(-10) \ F`

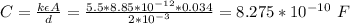
Maximum potential difference:

V = E x d

V = 200000 x 2 x 10⁻³ = 400 V

Maximum energy that can be stored in the capacitor:

E = ¹/₂CV²

E = ¹/₂ x 8.275 x 10⁻¹⁰ x (400)²

E = 6.62 x 10⁻⁵ J

Therefore, the maximum energy that can be stored in the capacitor is 6.62 x 10⁻⁵ J