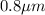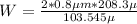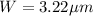Question

A particular NMOS device has parameters VT N = 0.6 V, L = 0.8µm, tox = 200 Å, and µn = 600 cm2 /V–s. A drain current of ID = 1.2 mA is required when the device is biased in the saturation region at VGS = 3 V. Determine the required channel width of the device.

Answer 1

`W= 3.22 \mu m`

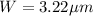
Step-by-step explanation:

the transistor In saturation drain current region is given by:

`i_D}=K_a(V_(GS)-V_(IN))^2`

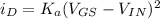
Making
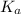`K_a` the subject of the formula; we have:

`K_a=\frac {i_D} {(V_(GS) - V_(IN))^2}`

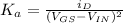
where;

`i_D = 1.2m`

`V_(GS)= 3.0V`

`V_(TN) = 0.6 V`

`K_a=\frac {1.2m} {(3.0 - 0.6)^2}`

`K_a = 208.3 \mu A/V^2`

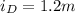
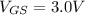
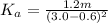
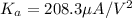
Also;

`k'_n}=(\mu n ((cm^2)/(V-s) ) \epsilon _(ox)((F)/(cm) ) )/(t_(ox)(cm))`

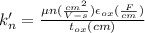
where:

`\mu n ((cm^2)/(V-s) ) = 600`

`\epsilon _(ox)=3.9*8.85*10^(-14)`

`{t_(ox)(cm)=200*10^(-8)`

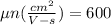
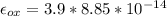
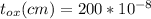
substituting our values; we have:

`k'_n}=((600)(3.988.85*10^(-14)))/((200*10^(-8)))`

`k'_n}=103.545 \mu A/V^2`

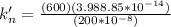
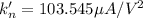
Finally, the width can be calculated by using the formula:

`W= (2LK_n)/(k'n)`

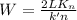
where;

L =
`0.8 \mu m`

`W= (2*0.8 \mu m *208.3 \mu)/(103.545 \mu)`

`W= 3.22 \mu m`