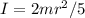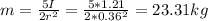Answer:
23 kg
Step-by-step explanation:
We can convert 160 revolution to radians knowing that each revolution is 2π rad.
Total angle swept is
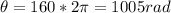
Since it starts from rest, from the following equation of motion we can calculate the constant angular acceleration.
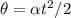
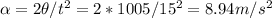
According to Newton's2nd law, the moments of inertia of this sphere is
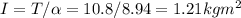
0.72 m in diameter = 0.72/2 = 0.36 m in radius
Since it's a solid sphere, the following formula can be applied for its moment of inertia: