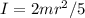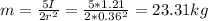Question

0.72-m-diameter solid sphere can be rotated about an axis through its center by a torque of 10.8 m • N which accelerates it uniformly from rest through a total of 160 revolutions in 15.0 s. What is the mass of the sphere? (ans: 23 kg)

Answer 1

23 kg

Step-by-step explanation:

We can convert 160 revolution to radians knowing that each revolution is 2π rad.

Total angle swept is
`\theta = 160*2\pi = 1005 rad`

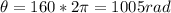
Since it starts from rest, from the following equation of motion we can calculate the constant angular acceleration.

`\theta = \alpha t^2/2`

`\alpha = 2\theta/t^2 = 2*1005/15^2 = 8.94 m/s^2`

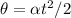
According to Newton's2nd law, the moments of inertia of this sphere is

`I = T / \alpha = 10.8 / 8.94 = 1.21 kgm^2`

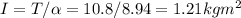
0.72 m in diameter = 0.72/2 = 0.36 m in radius

Since it's a solid sphere, the following formula can be applied for its moment of inertia:

`I = 2mr^2/5`

`m = (5I)/(2r^2) = (5*1.21)/(2*0.36^2) = 23.31 kg`