Ratio of areas of similar triangles is 9 : 25.
Solution:
Given data:
Ratio of sides of two similar triangles = 3 : 5
To find the ratio of areas of the triangles:
We know that,
In two triangles are similar, then the ratio of their area is equal to the square of the ratio of their sides.
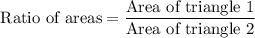
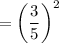
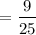
Ratio of areas of similar triangles is 9 : 25.