Answer:
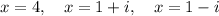
(one real zero and 2 complex zeros)
Explanation:
Given polynomial:
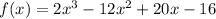
According to the Factor Theorem, if f(4) = 0 then (x - 4) is a factor of the given polynomial.
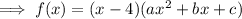
Expand the brackets:
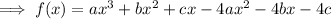
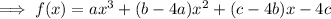
Compare coefficients with the given polynomial:
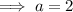
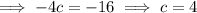
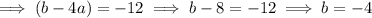
Substitute the found values of a, b and c:
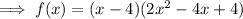
To find the zeros of f(x), set the function to zero and solve for x:
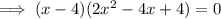
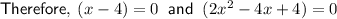
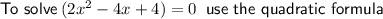
Quadratic Formula
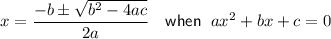
Therefore:
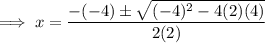
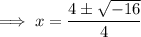
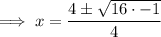
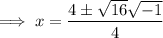
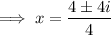
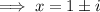
Therefore, the zeros of the function are:
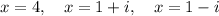
(one real zero and 2 complex zeros)