Question

Juana slides a crate along the garage floor. The coefficient of kinetic friction between the crate and the floor is 0.120. The crate has a mass of 56.8 kg and Juana pushes with a horizontal force of 124 N. If 95.7 J of total work are done on the crate, how far along the floor does it move?

Answer 1

To solve this problem it will be necessary to apply the Theorem of the work. The work theorem warns that energy in the form of work is equivalent to the product between the force and the displacement of the body. In mathematical terms this can be described as

`W = F\Delta x`

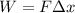
Here,

W = Work

F = Force

`\Delta x` = Displacement

Now the net force on the body is equivalent to the force applied to it minus the force produced by friction, therefore

`F = 124N -f_k`

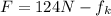
Remember also that the friction force is equal to the Normal Force for the frictional coefficient, then

`N = mg`

`f_k = \mu_k N`

`f_k = \mu_k (mg)`

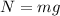
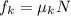
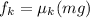
Replacing,

`f_k = (0.12)(56.8kg)(9.8m/s^2)`

`f_k = 67N`

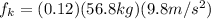
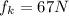
Replace the value and we have that

`F = 124N-67N`

`F = 57N`

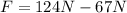
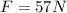
Rearranging the expression of work done for displacement and solving we have,

`\Delta x = (W)/(F)`

`\Delta x = (95.7J)/(57N)`

`\Delta x = 1.679m`

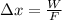
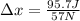
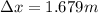
Therefore the crater moves on the van floor about 1.679m