Answer:
The chance that their average time is less than 9.5 minutes is 0.0094
Explanation:
X is the time it takes a randomly chosen clerical worker in an office to type and send a standard letter of recommendation
We are given that X has a normal distribution
Mean
 = 10.5 minutes
= 10.5 minutes
Standard deviation
 = 3 minutes
= 3 minutes
n = 50
We are supposed to find the chance that their average time is less than 9.5 minutes i.e. P(X<9.5 minutes)
Formula :
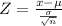
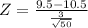
Z = −2.35
Refer the z table for p value
p value=0.0094
So, P(X<9.5)=P(Z<−2.35)=0.0094
Hence the chance that their average time is less than 9.5 minutes is 0.0094.