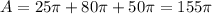Question

A container is in the shape of a cylinder with a hemisphere on the top. The cylinder has radius 5 cm and height 8 cm. The hemisphere has the same radius as the cylinder.

What is the total surface area of the container? Give your answer in cm2 correct to 3 significant figures.

Answer 1

The total surface area is given by:

• The base of the cylinder
• The lateral surface of the cylinder
• The surface of the hemishpere

The base of the cylinder is a circle with radius 5cm, so its area is

`A=\pi r^2=25\pi`

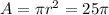
The lateral surface of the cylinder is a rectangle whose base is the circumference of the base circle, and whose height is the height of the cylinder. So, its area is

`A=b\cdot h=2\pi r\cdot h = 10\pi\cdot 8=80\pi`

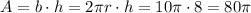
Finally, the surface of a sphere is given by

`A=4\pi r^2`

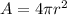
so, half that surface will be

`A=2\pi r^2=50\pi`

And the total surface area will be the sum of the three areas:

`A=25\pi+80\pi+50\pi = 155\pi`

Answer 2

Total surface area of the figure
`=486.7cm^2`

Explanation:

Total surface area of the figure= Surface area of cylinder + Area of the top hemisphere

`r= 5cm\\\\h= 8cm`

Area of the cylinder with the side walls and the the bottom:

`A=(2*\pi* r*h)+(\pi *r^2)`

`=(2*3.14*5*8)+(3.14*5*5)\\\\ =251.2+78.5\\\\ = 329.7 cm^2`

Area of the top hemisphere:

`2*\pi *r^2`

`=2*3.14*5*5`

Area of the top hemisphere=
`157 cm^2`

Total surface area of the figure
`= 329.7+157\\\\`

`=486.7cm^2`