Question

AX and EX are secant segments that intersect at point X. Circle C is shown. Secants A X and E X intersect at point X outside of the circle. Secant A X intersects the circle at point B and secant E X intersects the circle at point E. The length of A B is 7, the length of B X is 2, and the length of X D is 3. What is the length of DE? 1 unit 3 units 4One-half units 4Two-thirds units

Answer 1

the answer is b 3 units

Explanation:

Answer 2

DE = 3 units

Explanation:

The image is attached.

There are 2 secant lines in the circle. We can use secant theorem to solve this easily.

It states that "if 2 secants are drawn to a circle from an outside point, then product of 1 secant and its "outside" part is equal to product of other secant and its "outside" part.

From the figure, we can say:

AX * BX = EX * DX

We let the length to find , DE, be "x".

Thus, we can write:

`AX * BX = EX * DX\\(7+2)(2)=(x+3)(3)`

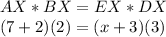
Now, we solve this for x:

`(7+2)(2)=(x+3)(3)\\(9)(2)=(3)(x+3)\\18=3x+9\\3x=18-9\\3x=9\\x=3`

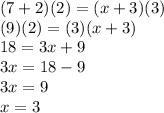
Thus,

DE = 3 units