Question: Find, separately, them mass of the balloon and the basket (incidentally, most of the balloon's mass is air)
Answer:
The mass of the balloon is 2295 kg, and the mass of the basket is 301 kg.
Step-by-step explanation:
Let us call the mass of the balloon
 and the mass of the basket
and the mass of the basket
 , then according to newton's second law:
, then according to newton's second law:
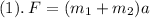 ,
,
where
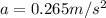 is the upward acceleration, and
is the upward acceleration, and
 is the net propelling force (counts the gravitational force).
is the net propelling force (counts the gravitational force).
Also, the tension
 in the rope is 79.8 N more than the basket's weight; therefore,
in the rope is 79.8 N more than the basket's weight; therefore,
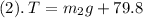
and this tension must equal
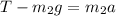

Combining equations (2) and (3) we get:
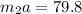
since
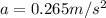 , we have
, we have

Putting this into equation (1) and substituting the numerical values of
 and
and
 , we get:
, we get:
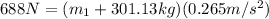

Thus, the mass of the balloon and the basket is 2295 kg and 301 kg respectively.