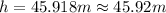Answers:
a) 5400000 J
b) 45.92 m
Step-by-step explanation:
a) The kinetic energy
 of an object is given by:
of an object is given by:
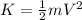
Where:
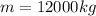 is the mass of the train
is the mass of the train
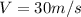 is the speed of the train
is the speed of the train
Solving the equation:
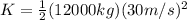
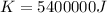 This is the train's kinetic energy at its top speed
This is the train's kinetic energy at its top speed
b) Now, according to the Conservation of Energy Law, the total initial energy is equal to the total final energy:
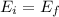
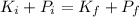
Where:
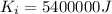 is the train's initial kinetic energy
is the train's initial kinetic energy
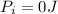 is the train's initial potential energy
is the train's initial potential energy
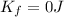 is the train's final kinetic energy
is the train's final kinetic energy
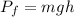 is the train's final potential energy, where
is the train's final potential energy, where
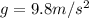 is the acceleration due gravity and
is the acceleration due gravity and
 is the height.
is the height.
Rewriting the equation with the given values:
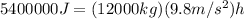
Finding
 :
: