Answer:
Thus, the induced current in the coil at
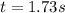 is 9.98 A.
is 9.98 A.
Step-by-step explanation:
Faraday's law says
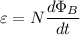
where
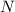 is the number of turns and
is the number of turns and
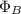 is the magnetic flux through the square coil:
is the magnetic flux through the square coil:
Now,
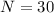
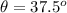
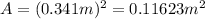
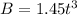 ;
;
therefore,
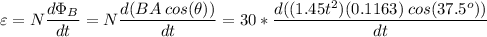
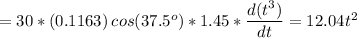
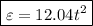
is the emf induced in the coil.
Now, the loop is connected to
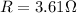 resistance; therefore, at
resistance; therefore, at
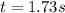
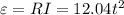
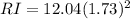
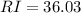
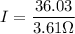
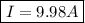
Thus, the current in the coil at
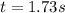 is 9.98 A.
is 9.98 A.