Question

An 30-turn coil has square loops measuring 0.341 m along a side and a resistance of 3.61 Ω. It is placed in a magnetic field that makes an angle of 37.5° with the plane of each loop. The magnitude of this field varies with time according to B = 1.45t^3, where t is measured in seconds and B in teslas. What is the induced current in the coil at t = 1.73 s?

Answer 1

Thus, the induced current in the coil at
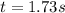`t =1.73s` is 9.98 A.

Step-by-step explanation:

Faraday's law says

`$\varepsilon = N (d \Phi_B)/(dt) $`

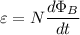
where
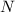`N` is the number of turns and
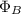`\Phi_B` is the magnetic flux through the square coil:

Now,

`N = 30`

`\theta = 37.5^o`

`A = (0.341m)^2= 0.11623m^2`

`B = 1.45t^3`;

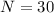
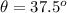
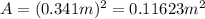
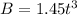therefore,

`$\varepsilon = N (d \Phi_B)/(dt) = N(d ( BA\:cos(\theta)))/(dt) = 30*(d ( (1.45t^2)(0.1163)\:cos(37.5^o)))/(dt)$`

`=30*(0.1163)\:cos(37.5^o)*1.45*(d ( t^3))/(dt) = 12.04t^2`

`\boxed{\varepsilon = 12.04t^2}`

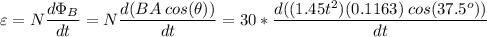
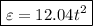
is the emf induced in the coil.

Now, the loop is connected to
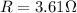`R = 3.61\Omega` resistance; therefore, at
`t = 1.73s`

`\varepsilon = RI = 12.04t^2`

`RI = 12.04(1.73)^2`

`RI = 36.03`

`I = (36.03)/(3.61\Omega )`

`\boxed{I = 9.98A }`

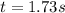
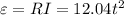
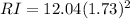
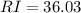
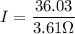
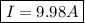
Thus, the current in the coil at
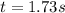`t =1.73s` is 9.98 A.