Answer:
Step-by-step explanation:
The answer choices are:
Solution
The remainder theorem states that the remainder of the division of a polynomial f(x) by a factor x - a is equal to f(a).
Therefore, when f(a) = 0, the remainder is zero and x - a is a factor of the polynomial.
Then, you must find f(a) for each of the factors on the choices:
a. x + 5
⇒ a = - 5
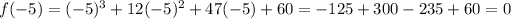
Since f(-5) = 0, x + 5 is a factor of the polynomial.
b. x + 4
⇒ a = - 4
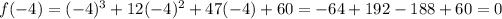
Since f(-4) = 0, x + 4 is a factor.
c. x + 3
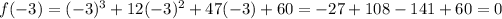
Since f(-3) = 0, x + 3 is a factor.
d. x + 2

Since f(-2) ≠ 0, x + 2 is not a factor ← answer