Question

Use the remainder theorem to find which of the following is not a factor of X^3+12X^2+47X+60

Answer 1

x+2

Step-by-step explanation:

Answer 2

• x + 2 is not a factor

Step-by-step explanation:

The answer choices are:

• a. x + 5

• b. x + 4

• c. x + 3

• d. x + 2

Solution

The remainder theorem states that the remainder of the division of a polynomial f(x) by a factor x - a is equal to f(a).

Therefore, when f(a) = 0, the remainder is zero and x - a is a factor of the polynomial.

Then, you must find f(a) for each of the factors on the choices:

a. x + 5

⇒ a = - 5

`f(-5)=(-5)^3+12(-5)^2+47(-5)+60=-125+300-235+60=0`

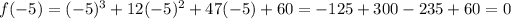
Since f(-5) = 0, x + 5 is a factor of the polynomial.

b. x + 4

⇒ a = - 4

`f(-4)=(-4)^3+12(-4)^2+47(-4)+60=-64+192-188+60=0`

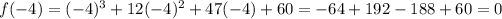
Since f(-4) = 0, x + 4 is a factor.

c. x + 3

`f(-3)=(-3)^3+12(-3)^2+47(-3)+60=-27+108-141+60=0`

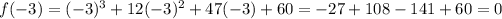
Since f(-3) = 0, x + 3 is a factor.

d. x + 2

`f(-2)=(-4)^3+12(-2)^2+47(-2)+60=-8+48-94+60=6`

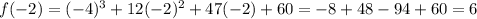
Since f(-2) ≠ 0, x + 2 is not a factor ← answer